GPU-Accelerating a Neutron Scattering Simulation with CUDA

⊕

Small angle neutron scattering for materials research uses a high-energy particle accelerator to produce scattering amplitude functions. However, the physics behind the neutron scattering is well-known and can be simulated on supercomputer clusters, provided an initial seed trajectory and molecular (MD) information is given.

I recently completed a project where I improved the performance of a program for neutron scattering physics simulation by using CUDA to get some quite large performance gains. Despite the existing application already being written for super-computer clusters with MPI, writing a CUDA scattering implementation, offloading some nodes to the GPU, and allowing for a “hybrid” CPU/GPU computation model that still supports CPU clusters worked surprisingly well.

In the blog, I’ll give some of the physics context behind the program, why neutron scattering simulations are even needed, and then finally talk about how exactly the CUDA implementation worked.

The Theory

Neutron scattering is a technique used to probe the atomic structure of materials by directing a beam of neutrons at a sample and analysing the way that these neutrons scatter. The well-known X-ray scattering technique is commonplace in science, but neutrons have the advantage of being neutrally charged, which means they can penetrate much deeper into the material. They also interact directly with the nuclei of atoms, rather than the electron clouds. This gives researchers a complementary technique to study e.g. diffusive or vibrational properties of materials. Researchers typically study the overall scattering amplitude graph, which determines where the scattered neutrons “end up”. These techniques are useful in domains such as crystallography, where the positions of the peaks in the graph determine important constants such as the structure factor of the material.

In the Born approximation, the total scattering amplitude is calculated as the sum of the contributions of all N individual scatterers, i.e. atoms. Given a position vector r_n(t) provided by the “seeding” molecular dynamics (MD) simulation, the overall amplitude arises from the constructive interference amplitudes, which is calculated as:

A(q, t) = ∑_{n ∈ {1, …, N}} ⋅ b_n(q) ⋅ e^iq ⋅ r_n(t)

for a scattering vector q given the atomic prefactor b_n(q). For neutron scattering this is a fixed constant. For X-rays it is calculated as

$$b_n (\bm{q}) = \sum_{j = 1}^{x} c_j \cdot e^{- d_j \cdot {\|\bm{q}\|}^2}$$

where c_j and d_j are tabulated constants. The other relevant equation in scattering theory is the associated total scattering intensity, which is given by

F(q, t) = A(q, t) ⋅ A^*(q, t)

where A^*(q, t) is the complex conjugate of A(q, t). However, in certain experiments, e.g. involving liquids, the sample may be isotropic, that is its properties are the same in all directions. Therefore, the scattering intensity becomes independent of the specific direction of q and only depends on the magnitude, which usually requires averaging the signal over all possible orientations of q. Similarly, in experiments focusing on the dynamics of the system, such as inelastic neutron scattering, the average behaviour of the system over a timescale is of interest and therefore requires summing the signal over time.

Although these operations are all computationally simple, the large data-sets mean that effective use of modern computer hardware is highly important. Specifically, programs for computing these scattering intensities must be massively parallelisable in order to scale well on multi-core machines and even clusters. Furthermore, in high-performance computing on many threads, careful attention must be paid to memory access patterns in order to make the most effective use of limited throughput between memory and processors.

Several programs to perform these tasks in a scalable manner have been written, including Sassena. This program was written to scale effectively on large supercomputers such as the Jaguar Cray XT5 at Oak Ridge National Laboratory, which it does by using MPI process-based parallelism as well as thread-based parallelism. Although the software was designed for high-performance in mind, the target platforms for which it was developed were primarily supercomputers from the early 2010s, many of which do not exist any more. Furthermore, the architecture of modern clusters have changed since then, particularly with the introduction of general-purpose graphics card programming (GPGPUs), meaning that programs which use a hybrid of CPU and GPU code can be run on them. A hypothesis of this report was that creating implementations which are able to run on graphics cards (e.g. using NVIDIA’s CUDA) would significantly improve the performance of Sassena due to the much larger thread-count of GPUs.

The Previous (CPU) Implementation

The main hypothesis was that implementing scattering on GPUs would lead to performance increases over the CPU implementation. This was because in roof-line analyses using perf, it was determined that although the CPU implementation showed strong scaling up to 24 cores, it had become bound by memory throughput limitations, meaning that any further increase in thread count would not improve performance as the processors would simply be idling while they wait for memory transfer operations to complete.

Let’s look at the general flow of the CPU implementation for self-scattering and how we transform this time signal into the desired output. It’s all based around OOP of course (very popular in the 2010s!) and implemented in the SelfVectorsScatterDevice class:

fftw_complex *SelfVectorsScatterDevice::scatter(size_t mi, size_t ai)
{
    double s = scatterfactors.get(assignment_[ai]);
    // double allocate (2*NF), to allow direct application of autocorrelation.
    size_t NTHREADS = worker_threads.size();
    size_t offset = (mi % NTHREADS) * 2 * NF;

    fftw_complex *p_at_local = &(at_[offset]);

    double qx = subvector_index_[mi].x;
    double qy = subvector_index_[mi].y;
    double qz = subvector_index_[mi].z;

    coor_t *p_data = &(p_coordinates[ai * NF * 3]);

    for (size_t j = 0; j < NF; ++j) {
        coor_t x1 = p_data[j * 3];
        coor_t y1 = p_data[j * 3 + 1];
        coor_t z1 = p_data[j * 3 + 2];

        double p1 = x1 * qx + y1 * qy + z1 * qz;
        double sp1 = sin(p1);
        double cp1 = cos(p1);
        p_at_local[j][0] = s * cp1;
        p_at_local[j][1] = s * sp1;
    }

    memset(&p_at_local[NF], 0, NF * sizeof(fftw_complex));

    return p_at_local;

The scatter function is the heart of the algorithm. We’re calculating a_i(t) = s_i ⋅ exp (iq ⋅ r_i(t)) here, namely the phase of the scattering amplitude for each incoming scattering vector q and each atom i over every frame in 1…NF. Because the program can be run on multiple hardware threads (on a single MPI node), we need to calculate an offset in the output buffer at_ and the input data.

This a_i(t) signal needs to be further processed depending on the use-case of the program. Autocorrelate computes the time autocorrelation of the amplitude signal, which gives us the intermediate scattering function F_s(q, τ), which is often used in hydrogen-dominated incoherent dynamics. By contrast, square computes the function |a_i(t)|², which is the time-independent “self intensity” per atom. Finally, there’s a plain DSP, which just sums A(t) = ∑_ia_i(t).

void SelfVectorsScatterDevice::dsp(fftw_complex *at)
{
    if (Params::Inst()->scattering.dsp.type == "autocorrelate") 
    {
            fftw_execute_dft(fftw_plan_fwd_, at, at);
            for (size_t i = 0; i < 2 * NF; ++i) {
                at[i][0] = at[i][0] * at[i][0] + at[i][1] * at[i][1];
                at[i][1] = 0;
            }
            fftw_execute_dft(fftw_plan_backwd_, at, at);
            for (size_t i = 0; i < NF; ++i) {
                double factor = (1.0 / (2 * NF * (NF - i)));
                at[i][0] *= factor;
                at[i][1] *= factor;
            }
        }
    } else if (Params::Inst()->scattering.dsp.type == "square") {
        size_t NF = N;
        for (size_t n = 0; n < NF; n++) {
            double r = at[n][0] * at[n][0] + at[n][1] * at[n][1];
            at[n][0] = r;
            at[n][1] = 0;
        }
    }
    // plain removed as it does nothing!
    // error checking removed for clarity
}

The final step is to reduce all of these at_ signals into additional afinal and a2final signals for the HDF5 output. These sum or sum and square the signal over all NF time-frames respectively.

void SelfVectorsScatterDevice::store(fftw_complex *at)
{
    complex<double> a = smath::reduce<double>(at, NF) * (1.0 / NF);
    afinal_ += a;
    a2final_ += a * conj(a);
    smath::add_elements(atfinal_, at, NF);
}

Designing a Scattering System in CUDA

If the memory was bound by operations such as transferring coordinates and scattering factors, then more scaling might be possible on the GPU! This is because once data has been transferred onto global video RAM (VRAM), it is possible for certain memory accesses to be coalesced by the CUDA runtime, meaning that data requests from multiple threads are efficiently combined into a single transaction. If coalesced properly, then the memory throughput of the program can approach the theoretical peak memory bandwidth of the GPU, which is usually much higher than for CPUs.

In order to verify the hypothesis, I first chose to implement self-scattering instead of all-scattering in CUDA as it is relatively simpler. Additionally, the most important DSP type to implement in self-scattering is autocorrelation as this corresponds to dynamic incoherent scattering, which is more important in most use-cases of the program. Autocorrelation is ordinarily an O(N²) algorithm for a signal of length N, as it involves calculating the product of a signal with all of its possible time-shifts. However, by computing the discrete Fourier transform (DFT), multiplying this with the complex conjugate of the signal and then computing the inverse DFT, it can be calculated in O(NlogN) time. Highly optimised libraries for calculating DFTs exist in CUDA, such as cuFFT, and particularly for high dimensional DFTs, these implementations can be faster than on the CPU. It also kept the overall system simpler as writing a high-performance FFT on the GPU is a complicated topic.

It was decided to base the implementation of self-scattering on a task-based model instead of traditional thread-based programming as had been used previously in Sassena. This allows for encapsulating each stage of the scattering process as a task and letting the task manager determine the optimal allocation of threads and streaming multi-processors to each task. The library chosen for this was Taskflow. Furthermore, Taskflow allows for creating a computational graph either at compile-time or runtime and then dispatching the entire graph to the GPU in one step. This decreases latency over launching each kernel (i.e. essentially a function run on the GPU) one after the other in C++, as no communication is needed with the CPU once the graph has been dispatched.

⊕

The task graph created by Taskflow and dispatched to the GPU for self-scattering with autocorrelation at runtime. The entire process is built around three stages. First is the self-scattering kernel, which calculates amplitudes according to the Born approximation. Then, it's sent to the DSP layer, which has various modes like autocorrelate or square. Finally, both store_atfinal and store are reduction kernels to get our final amplitude function.

In this implementation of self-scattering, it was decided to continue the previous model of calculating multiple orientational averaging vectors in parallel, but also to further increase parallelism by calculating the contribution of several atoms in parallel for the scattering intensity. This meant the core loop of the program became

for (n = 0; n < assignment.size(); n += ATOM_BLOCK) {
  tf::cudaFlow flow; // a computational graph
  for (atom = 0; atom < std::min(ATOM_BLOCK,assignment.size()-n);atom++) {
    for (i = 0; i < NM; i += AVG_BLOCK) {
      size_t N = std::min(AVG_BLOCK, NM-i);
      dim3 blockDim = dim3(32, 32); // a fixed 1024 block of threads
      // N in the x-axis, NF in the y-axis.
      // Additional division as N % blockDim.x != 0 possible
      dim3 single_at_grid((N + blockDim.x - 1) / blockDim.x,
                          (NF + blockDim.y - 1) / blockDim.y);
      auto zero_dat = cudaflow.memset(at[id], 0,
                    2 * NF * N * sizeof(complex));
      // create scattering kernel and provide it with threads
      auto kernel = flow.kernel(single_at_grid, blockDim_, 0,
                  sass::cuda::cuda_scatter, ...).name("self_scatter");
      kernel.succeed(zero_dat); // define the edges of the graph
      // continue building graph with DSP and reduction kernels next...
    }
  }
  // Send cudaflow to the gpu and execute
  cudaflow.run(stream);
  stream.synchronize();
}

Although Taskflow manages the allocation and scheduling of kernels onto processors on the GPU, it is still necessary to define how many threads are desired for each kernel. In contrast to the CPU, where each processor has several cores (e.g. 16) and where each core is able to run one thread at a time, GPUs contain significantly more cores, typically at least 60. Moreover, each core runs several threads at a time, called a warp, which is typically 32 threads. On each processor in the GPU, a larger number of threads can be created (usually 1024 and called a thread block) and the execution of these is interleaved to hide the latency of memory accesses.

⊕

Thread structure in CUDA. Source: CUDA Developer Guide.

Threads on the GPU are structured on a two-dimensional coordinate system and it is up to the programmer to use this information to create a sensible partition of the work amongst these threads. In Sassena, the convention that the x-axis would correspond to N, the number of orientational averaging vectors in the block (from a total N_M) and the y-axis would correspond to N_F, the number of frames in the MD simulation, was used.

As stated, in order to use these threads, the algorithm in each kernel must be written so that each thread is assigned work and does not interfere with the work of other threads.

__global__ void sass::cuda::cuda_scatter(...)
{
    // Calculate the thread index in the 2D grid
    size_t idx = blockIdx.x * blockDim.x + threadIdx.x;
    size_t jdx = blockIdx.y * blockDim.y + threadIdx.y;
    if (idx < N && jdx < NF) {
        size_t offset = idx * 2 * NF; // as 2 copies of data for autocorrelation
        const size_t qindex = index + idx; // sub-vector index
        const double s = scatterfactors[aindex]; // b_n
        complex *p_at_local = &(at[offset]); // output buffer
        // q vec
        const double qx = subvector_index[qindex].x;
        const double qy = subvector_index[qindex].y;
        const double qz = subvector_index[qindex].z;
        // r_n
        coor_t *p_data = &(p_coords[aindex * NF * 3]);
        const coor_t x1 = p_data[jdx * 3];
        const coor_t y1 = p_data[jdx * 3 + 1];
        const coor_t z1 = p_data[jdx * 3 + 2];
        // x^T * q
        const double p1 = x1 * qx + y1 * qy + z1 * qz;
        double cp1, sp1;
        sincos(p1, &sp1, &cp1);
        p_at_local[jdx][0] = s * cp1; // re
        p_at_local[jdx][1] = s * sp1; // im
    }
}

Because of our choice of coordinate system, this meant that each kernel must calculate two unique indices idx and jdx and the allocated threads may span multiple thread blocks. It is further important to note that an additional offset variable is needed to skip the second copy of the signal, which is created due to autocorrelation. Additional kernels were also needed for DSP tasks. These repeat this pattern. For example, as part of the autocorrelation, the power spectrum of the signal is calculated (typically be referred to as the dynamic structure factor in the neutron scattering literature):

// For DSP type "autocorrelate"
__global__ void sass::cuda::autocorrelate_pow_spect(complex *at, size_t N, size_t NF)
{
    // Calculate the thread index in the 2D grid
    size_t idx = blockIdx.x * blockDim.x + threadIdx.x;
    size_t jdx = blockIdx.y * blockDim.y + threadIdx.y;
    if (idx < N && jdx < 2 * NF) {
        size_t offset = idx * 2 * NF;
        complex *data = &(at[offset]); // get subvector
        data[jdx][0] = data[jdx][0] * data[jdx][0] + data[jdx][1] * data[jdx][1];
        data[jdx][1] = 0;
    }
}

However, in this example, jdx needs to range over both copies of the signal, so here the kernel is launched on a larger grid:

// We need twice as many threads because we need 2*NF for the autocorrelation
// in the y-axis.
dim3 double_at_grid((N + blockDim_.x - 1) / blockDim_.x,
                    (2 * NF + blockDim_.y - 1) / blockDim_.y);

Other DSP functions are also available, though these are simpler:

// For DSP type "square"
__global__ void sass::cuda::square_elements(fftw_complex *at, size_t N, size_t NF)
{
    // Calculate the thread index in the 2D grid
    size_t idx = blockIdx.x * blockDim.x + threadIdx.x;
    size_t jdx = blockIdx.y * blockDim.y + threadIdx.y;

    if (idx < N && jdx < NF) {
        size_t offset = idx * 2 * NF;

        // Point to the specific element within the subvector
        fftw_complex *data = &(at[offset]);

        double r = data[jdx][0] * data[jdx][0] + data[jdx][1] * data[jdx][1];
        data[jdx][0] = r;
        data[jdx][1] = 0;
    }
}

// For DSP type "autocorrelate"
__global__ void sass::cuda::autocorrelate_normalize(fftw_complex *at, size_t N, size_t NF)
{
    // Calculate the thread index in the 2D grid
    size_t idx = blockIdx.x * blockDim.x + threadIdx.x;
    size_t jdx = blockIdx.y * blockDim.y + threadIdx.y;

    if (idx < N && jdx < NF) {
        size_t offset = idx * 2 * NF;
        // get subvector
        fftw_complex *data = &(at[offset]);

        double factor = (1.0 / (2.0 * NF * (NF - jdx)));
        data[jdx][0] *= factor;
        data[jdx][1] *= factor;
    }
}

Excluding the coordinate and scattering factors arrays, the most important data structure in the self-scattering implementation was the signal buffer, which was accessed as the array cpp complex* at in the above code snippets. This buffer has size 2 ⋅ N_F ⋅ N ⋅ d, where d= sizeof(complex) and N is the number of orientational averaging vectors in one block. The buffer contains the contribution of one atom to the overall output for each time step and orientational averaging vector in the block. Because the number of orientational averaging vectors stays constant over the life of the program, we can pre-allocate these signal buffers before scattering begins, re-use them for each iteration of the outer-most ATOM_BLOCK loop and delete them when the program ends. This is significantly more efficient than re-allocating these buffers for each iteration.

Furthermore, if the DSP type was autocorrelation, the same scheme is used for pre-allocating the working memory for the DFTs. For both of these allocations, a simple id numbering scheme is employed.

// Create at_ptrs and fft_handles in advance and re-use them
cr_id = 0; // creation ID used to keep track of the at_ptrs and fft_handles
for (n = 0; n < std::min(ATOM_BLOCK, assignment.size() - n); ++n) {
    for (size_t i = 0; i < NM; i += NTHREADS) {
        const size_t N = std::min(NTHREADS, NM - i); // number of subvectors in block
        complex *d = nullptr;
        cudaMalloc(&d, 2 * NF * N * sizeof(complex));
        at_ptrs[cr_id] = d;
        if (Params::Inst()->scattering.dsp.type == "autocorrelate") {
            // Create a DFT plan and store it
            cufftHandle dft; cufftCreate(&dft);
            auto res = cufftPlan1d(&dft, 2 * NF, CUFFT_Z2Z, N);
            if (res != CUFFT_SUCCESS)
                sass::err("Could not create a cuFFT plan for autocorrelation.");
            fft_handles[cr_id] = dft;
        }
        ++cr_id;
    } }

These buffers are then accessed when building the Taskflow tasks by calculating the id in exactly the same manner.

Now that the contribution of each atom to the scattering intensity is known, these signal buffers must be reduced into intermediate buffers so that they can be written into the final output values fq, fq2 and fqt in the HDF5 file format. As the parallelism of Sassena has now increased significantly in this implementation, careful attention must be paid to the reduction step as many simultaneous writes to a single location can cause data races. The naive synchronisation approach would be to use mutexes in this case. For CUDA code, it is more common to use the atomicAdd instruction instead of a mutex lock as it’s generally faster. However, even atomic instructions incur performance overhead as they force the serialisation of the instruction stream, which introduces contention.

One possible remedy to this problem is to use partial reduction, where an intermediate buffer is created in memory for each thread block. All threads in the thread block will then reduce into this intermediate buffer and only one thread in the buffer will use an atomicAdd instruction to write the intermediate buffer into the global buffer. This approach significantly reduces resource contention and was used in the new implementation for reducing to the afinal and a2final buffers, which eventually output to fq and fq2.

__global__ void sass::cuda::store(complex *afinal, complex *a2final,
complex *at, size_t N, size_t NF)
{
    extern __shared__ complex<double> shared_mem[];
    complex<double> *shared_a = shared_mem;
    complex<double> *shared_a2 = shared_mem + blockDim.x;
    if (threadIdx.x < N) {
        size_t offset = threadIdx.x * 2 * NF;
        complex *data = &(at[offset]); // get subvector
        auto a = complex<double>(0.0, 0.0);
        for (i = 0; i < NF; i++) {
            a += complex<double>(data[i][0], data[i][1]);
        }
        a *= 1.0 / NF;
        shared_a[threadIdx.x] = a;
        shared_a2[threadIdx.x] = a * conj(a);
        auto a2 = a * conj(a);
    } else {
        shared_a[threadIdx.x] = complex<double>(0.0, 0.0);
        shared_a2[threadIdx.x] = complex<double>(0.0, 0.0);
    }
    __syncthreads();
    if (threadIdx.x == 0) {
        complex<double> block_sum_a(0.0, 0.0);
        complex<double> block_sum_a2(0.0, 0.0);
        for (i = 0; i < blockDim.x; i++) {
            block_sum_a += shared_a[i];
            block_sum_a2 += shared_a2[i];
        }
        atomicAdd(&(afinal[0][0]), block_sum_a.real());
        atomicAdd(&(afinal[0][1]), block_sum_a.imag());
        atomicAdd(&(a2final[0][0]), block_sum_a2.real());
        atomicAdd(&(a2final[0][1]), block_sum_a2.imag());
    }
}

In the store kernel, the partial reduction technique to reduce to the intermediate buffers shared_a and shared_a2 was used. These are both created in block-level memory, meaning that accessing it is faster than global memory. We use the __syncthreads() function to wait until all threads in the block have finished. Finally, only the thread where threadIdx.x == 0 reduces the intermediate buffer into the global atfinal and a2final buffers.

Conclusion

⊕

A comparison of the new GPU implementation, running on an RTX 3080, when compared to a single-node implementation of the previous, CPU based, implementation with varying numbers (NP) of hardware threads used.

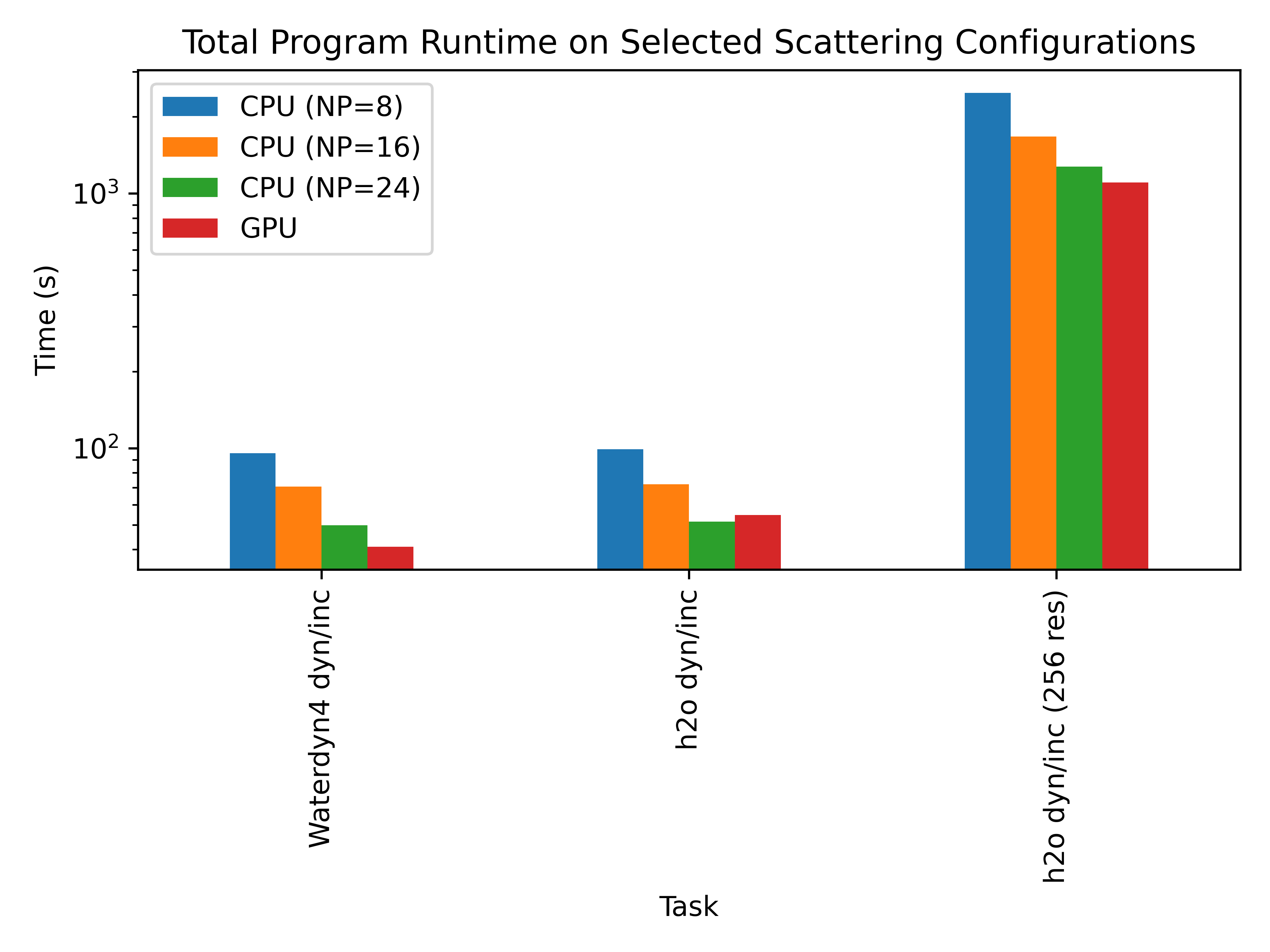
Overall the CUDA implementation significantly out performs the existing single-node CPU implementations of the self scattering kernel, as shown in the graph. However, the previous implementation supported MPI, which meant that the tasks could be split across many nodes in a supercomputer cluster. Luckily, the new CUDA implementation is directly “wired” into the existing MPI communication infrastructure, meaning that some nodes in the MPI cluster can use CPUs while others would be GPU nodes, giving us the ability to use both, which is known as a “hybrid” setup in the HPC world.